10050. Longest path in a tree

An undirected weighted tree is given. Find the longest path in it: identify two vertices such that the distance between them is maximized.

Input. The first line contains the number of vertices in the tree n (2 ≤ n ≤ 10⁵). The following n – 1 lines describe the edges. Each line contains three integers: the numbers of the vertices connected by an edge (vertices are numbered from 1 to n) and the weight w (2 ≤ w ≤ 10⁵) of the edge.

Output. Print the length of the longest path in the tree.

Sample input

Sample output

1 2 3

2 3 4

2 6 2

6 4 6

6 5 5

SOLUTION

graphs, breadth first search

Algorithm analysis

The shortest path in a weighted tree can be found using either depth-first search or breadth-first search; using Dijkstra’s algorithm is not necessary in this case.

To find the longest path (the diameter of the tree), proceed as follows:

1. Perform a breadth-first search starting from the first vertex. Identify the vertex v, which has the longest path from the starting vertex.

2. Next, perform a breadth-first search starting from vertex v to find the vertex u, which also has the longest path from v.

3. The path from v to u is the longest path in the tree (the tree’s diameter).

Example

The tree shown in the example has the following structure:

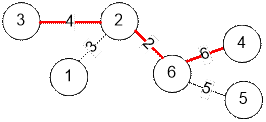
· Perform a breadth-first search starting from vertex 1 (left picture). The longest path will be to vertex 4.

· Then, perform a breadth-first search starting from vertex 4 (right picture). The longest path will be to vertex 3, and its length is 12.

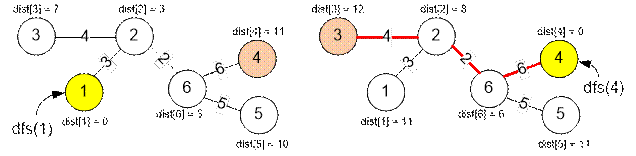
Algorithm implementation

Declare the adjacency list of the graph g.

Declare the array of shortest distances d.

vector<vector<pair<int, int>> > g;

vector<long long> d;

The function bfs performs a breadth-first search starting from vertex v.

int bfs(int v)

{

deque<int> q;

q.push_back(v);

while (!q.empty())

{

int v = q.front(); q.pop_front();

for (auto x : g[v])

{

int to = x.first;

int w = x.second;

if (d[to] == -1)

{

d[to] = d[v] + w;

q.push_back(to);

}

Return the number of the vertex to which the distance from vertex v is maximal.

return max_element(d.begin() + 1, d.begin() + n + 1) - d.begin();

}

The main part of the program. Read the input data. Build the graph.

scanf("%d", &n);

g.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d %lld", &b, &e, &dist);

g[b].push_back({ e, dist });

g[e].push_back({ b, dist });

}

Initialize the array of shortest distances.

d = vector<long long>(n + 1, -1);

d[1] = 0;

Perform the first breadth-first search starting from vertex 1. Identify the vertex v that is farthest from vertex 1.

int v = bfs(1);

Re-initialize the array of shortest distances and perform the second breadth-first search starting from vertex v.

d = vector<long long>(n + 1, -1);

d[v] = 0;

v = bfs(v);

Print the result – the length of the longest path.

printf("%lld\n", d[v]);

Algorithm implementation – depth first serch

The adjacency list of the graph is stored in the array g.

To store the shortest distances, declare the array dist.

vector<vector<pair<int, int>> > g;

vector<long long> dist;

The function dfs performs a depth-first search starting from vertex v. Vertex p is the parent of v during the depth-first search.

void dfs(int v, int p = -1)

{

Iterate over all edges adjacent to vertex v.

for (auto x : g[v])

{

Consider the edge v → to with weight w.

int to = x.first;

int w = x.second;

If to ≠ p, update dist[to] and perform a depth-first search starting from vertex to.

if (to != p)

{

dist[to] = dist[v] + w;

dfs(to, v);

}

The main part of the program. Read the input data. Build the graph.

scanf("%d", &n);

g.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d %d", &b, &e, &w);

g[b].push_back({ e, w });

g[e].push_back({ b, w });

}

Perform a depth-first search starting from vertex 1. Fill the array of shortest distances dist from vertex 1.

dist.assign(n + 1, -1);

dist[1] = 0;

dfs(1);

Find vertex v, which is the farthest from vertex 1.

v = max_element(dist.begin(), dist.end()) - dist.begin();

Perform a second depth-first search starting from vertex v. Fill the array of shortest distances dist from vertex v.

dist.assign(n + 1, -1);

dist[v] = 0;

dfs(v);

The largest value in the array dist is equal to the diameter of the tree.

v = max_element(dist.begin(), dist.end()) - dist.begin();

Print the answer.

printf("%lld\n", dist[v]);

Python implementation

from collections import deque

Read the input data. Store the adjacency list of the graph in g.

Declare a list of shortest distances d.

n = int(input())

g = [[] for _ in range(n + 1)]

d = [-1] * (n + 1)

Construct a graph.

for _ in range(n - 1):

b, e, dist = map(int, input().split())

g[b].append((e, dist))

g[e].append((b, dist))

The function bfs performs a breadth-first search starting from vertex v.

def bfs(v):

q = deque()

q.append(v)

while q:

v = q.popleft()

for to, w in g[v]:

if d[to] == -1:

d[to] = d[v] + w

q.append(to)

Return the number of the vertex that is farthest from vertex v.

return d.index(max(d))

Perform the first breadth-first search from vertex 1. Determine the vertex v that is the farthest from vertex 1.

d[1] = 0

v = bfs(1)

Initialize the array of shortest distances and perform the second breadth-first search from vertex v.